On,some,novel,solution,solutions,to,the,generalized,Schrödinger-Boussinesq,equations,for,the,interaction,between,complex,short,wave,and,real,long,wave,envelope

Dipnkr Kumr , Kmyr Hossini , Mohmm K.A.Kr , , Mlik Kpln ,Sohil Slhshour

a Department of Mathematics, Bangabandhu Sheikh Mujibur Rahman Science & Technology University, Gopalganj 8100, Bangladesh

b Department of Mathematics, Rasht Branch, Islamic Azad University, Rasht, Iran

c Institute of Mathematical Sciences, Faculty of Science, University of Malaya, Kuala Lumpur 50603, Malaysia

d Department of Mathematics, Art-Science Faculty, Kastamonu University, Kastamonu, Turkey

e Faculty of Engineering and Natural Sciences, Bahcesehir University, Istanbul, Turkey

ABSTRACT This paper explores some novel solutions to the generalized Schrödinger-Boussinesq (gSBq) equations,which describe the interaction between complex short wave and real long wave envelope.In order to derive some novel complex hyperbolic and complex trigonometric function solutions, the sine-Gordon equation method (sGEM) is applied to the gSBq equations.Novel complex hyperbolic and trigonometric function solutions are expressed by the dark, bright, combo dark-bright, W -shaped, M-shaped, singular,combo singular, and periodic wave solutions.The accuracy of the explored solitons is examined under the back substitution to the corresponding equations via the symbolic computation software Maple.It is found from the back substitution outcomes that all soliton solutions satisfy the original equations.The proper significance of the explored outcomes is demonstrated by the three-dimensional (3D) and two-dimensional (2D) graphs, which are presented under the selection of particular values of the free parameters.All the combo-soliton ( W -shaped, M -shaped, and periodic wave) solutions are found to be new for the interaction between complex short wave and real long wave envelope in laser physics that show the novelty of the study.Moreover, the applied method provides an efficient tool for exploring novel soliton solutions, and it overcomes the complexities of the solitary wave ansatz method.

Keywords:Generalized Schrödinger-Boussinesq equations Sine-Gordon expansion method Soliton solutions

There is no doubt that many scenarios in nature can be presented under the modeling of nonlinear partial differential equations (PDEs) with their explicit or numerical solutions.To understand such scenarios to nonlinear PDEs by their explicit solutions,many applied mathematicians, engineers, and scientists have their mutual interest to search for novel soliton solutions to nonlinear PDEs by analytical methods due to their important role and applicability in fluid mechanics, plasma physics, nonlinear optics,mathematical physics, and other related engineering sciences [1 , 2].The nonlinear Schrödinger’s (NLS) equation [3-9] , the resonant NLS equation [10] , the Schrödinger-Hirota equation [11 , 12], the Chen-Lee-Liu equation [13] , the ill-posed Boussinesq equation [14] , and the gSBq equations [15-31] are considered as the most important models related to such aforesaid research fields.

This paper focuses on the gSBq equations [15] , which are read as:

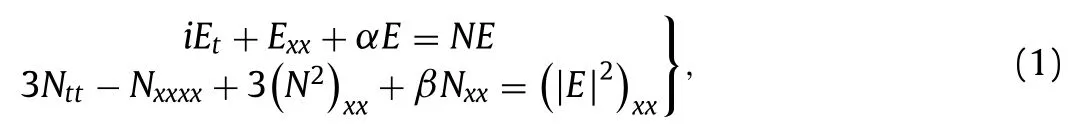
where αand βare real parameters, E( x, t ) is a complex function that specifies the complex Schrödinger field, and N( x, t ) is a real function that implies the real Boussinesq field.Equation (1) is one of the familiar models that explain the various physical impacts in the field of laser and plasma, such as the interaction of long waves with short wave packets in nonlinear dispersive media, the intense electromagnetic waves, the Langmuir soliton formation, and modulation instabilities [15-17] .With the aid of Painlevéanalysis,Chanda and Chowdhury [16] examined the integrality condition of the gSBq equations.Furthermore, in the past, several research studies have been conducted on constructing soliton solutions for a system of coupled gSBq equations via various analytical methods, such as the algebraic method [18] , the extended trial equation method [19] , the extended simplest equation method [20] ,the generalized Jacobi elliptic function method [21] , the extended coupled sub-equations expansion method [22] , the direct algebraic method [23] , the simplest equation method [24] , the improved tan ( Φ(ξ) / 2 ) -expansion method [25] , the method of dynamical systems [26] , two-soliton and homoclinic test methods [27] , the generalized Jacobi elliptic functions expansion method [28] , the improved general mapping deformation method [28] , the extended auxiliary function method [28] , the ( G ’ /G, 1 /G ) -expansion method[29] , the modified Kudrayshov method [30] , and the fractional natural decomposition method [31] (For more studies about fractional calculus and its applications, see [58-61] ).It is interesting to mention that gSB equations describe the interaction of long waves with short wave packets in nonlinear dispersive media.

Solitons are localized waves that propagate at a constant speed without changing their shape.They are caused by a cancellation of nonlinear and dispersive effects in the medium.They are observed in many well-known models of nonlinear dynamics for various shapes of wave solutions, such as dark, bright, envelope,compact on, periodic, singular, optical, Jacobi elliptic function, and many other forms.In order to extract the soliton solutions to the nonlinear evolution equations (NLEEs), there are several operative generalized or modified methods have been developed and performed.Some examples of the operative methods are the Bäcklund transformation [11] , the extended tanh expansion method[3 , 12], the solitary wave ansatz method [14] , the Riccati equation method [12] , the reduction of order method [32] , the He’s variational principle [32] , the Jacobi elliptic function method [7-9 , 33-36], the Bernoulli sub-ODE method [37] , the Riccati-Bernoulli sub-ODE method [14] , the generalized exp ( φ (ξ) ) -expansion method[38] , the first integral method [10] , the extended trial scheme approach [10] , the Kudryashov method [39] , the modified Kudryashov method [6 , 40-42], the generalized Kudryashov’s method [10 , 57],the ex p a -function method [6] , the auxiliary equation method [43] ,the new auxiliary equation method [44 , 45], the complex envelope function ansatz method [13] , the conservation laws [13] , the Lie symmetry method [37] , the sine-Gordon expansion method(sGEM) [5 , 46 , 47], and the extended sinh-Gordon equation method(EshGEM) [48-51] .Recently, by using Hirota soliton condition, Nsoliton solutions are computed by Hirota bilinear method for both local (1 + 1)-dimensional [52] and (2 + 1)-dimensional integrable equations [53-55] .The similar N-soliton solutions of the nonlocal integrable equations, namely Riemann-Hilbert problems in the reflectionless case, are obtained [56] .From [56] , the Riemann-Hilbert problems determine generalized Jost solutions of higher-order matrix spectral problems.The Sokhotski-Plemelj formula is used to transform the associated Riemann-Hilbert problems into Gelfand-Levitan-Marchenko type integral equations.

While some previous research work that have been conducted are essential to the field of ocean engineering and science such as the analytical and approximate solutions of nonlinear Schrödinger equation with higher dimensional anomalous dispersion regimes via the techniques of generalized Riccati equation mapping, and coupled q-homotopy analysis with Laplace transform [62] , solitary wave solutions for the proposed coupled nonlinear Schrödinger equations and Davey-Stewartson system with variable coefficients via the technique of sine-Gordon equation [63] , the Korteweg-De Vries (KdV) and Burgers equations’ numerical solution proposed in the Caputo fractional derivative’s (CFDr) sense via the method of local mesh less collocation [64] , the potential KdV and Benjamin equations’ solution proposed in the CFDr’s sense via the method of q -homotopy analysis transform [65] , exact solutions to essential nonlinear equations such as the modified KdV-Zakharov-Kuznetsov equation, Jimbo-Miwa equation, and 5 th -order KdV equation via the method of ( G’/G )-expansion [66] , and the generalized Hirota-Satsuma coupled KdV equations’ solutions proposed in the conformable derivative’s sense via the method of ( G’/G )-expansion[67] , our research study is totally original and with novel results where the main concentration in this work is to employ the sGEM of Eq.(1) .The sGEM has never been applied to solve the system in Eq.(1) .In the past, some research studies have been done on solving other systems of nonlinear PDEs by the sGEM [46 , 47 , 57-59].The sGEM is a robust and powerful technique that can be easily applied to both classical-integer and fractional order PDEs to construct various forms of soliton solutions, such as dark, bright,combined dark-bright, singular, combined singular soliton, and other solutions.It is remarkable to mention here that the sGEM overcomes the complexities of the solitary wave ansatz method[14 , 60].Therefore, our results paly an essential role in understanding very interesting nonlinear phenomena such as the interaction of long waves with short wave packets in nonlinear dispersive media which is considered very important in the field of ocean engineering and science because the obtained solutions of the studied equations are capable of investigating the mathematical model of gravity water waves in shallow water, plasma waves in coastal seas, and long waves in harbor [5-31] .As a result, the attained exact solutions of our research study will enrich all ocean engineers to validate the numerical simulation results for surface gravity water waves modeling in shallow water.

The key objective of this research is to construct some novel forms of explicit complex hyperbolic and complex trigonometric function solutions with the aid of the sGEM containing dark,bright, combined dark-bright, singular, combined singular, periodic wave, and other soliton solutions to the gSBq equations.

The organization of the paper is as follows.In Section 2 , we discuss in a step-by-step the sGEM.A mathematical analysis of the governing equations is presented in Section 3 .In Section 4 , we construct various forms of soliton solutions such as dark, bright,combined dark-bright, singular, W -shaped, M-shaped, combined singular optical, and periodic wave solutions via the sGEM.A general discussion and concluding remarks are presented in Section 5 .

A detailed explanation of the sGEM is presented in this section.To apply the sGEM, the following steps are needed to be followed[46] :

Step 1: A general form of the nonlinear PDE is considered containing two independent variables x and t , is given by

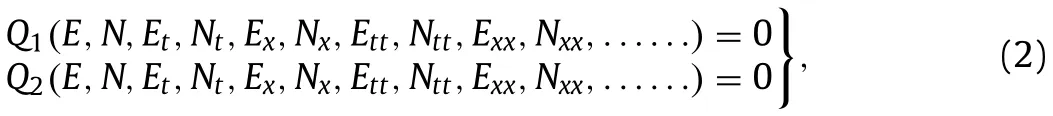
where E = E( x, t ) is a complex, and N = N( x, t ) is a real unknown function, Q1and Q2are polynomials in E( x, t ) and N( x, t ) , and their derivative with respect to tand x .It is mentioned that the highest order derivatives and nonlinear terms are involved in Eq.(2) .The subscripts stand for the partial derivatives.The main steps of the sGEM are as follows:

Adopting the complex transformation E( x, t ) = eiθU(η) ,N( x, t ) = V (η) , where θ= kx + ωt, and η= px + rt converts Eq.(2) to the following nonlinear ODE:

Fig.1.(a)-(b) 3D plots of the solutions | E( x, t )| and | N( x, t )| specified by Eq.(19) , and (c)-(d) 2D plots of (a)-(b), respectively.The dotted black, blue, and red lines indicate the variations of the mentioned solutions along t = -3 , t = 0 , t = 3 , respectively.

where, P1and P2are polynomials of U, V and their derivatives and the superscripts indicate the ordinary derivatives with respect to η.

Step 2: It is supposed that the formal solutions of Eq.(3) can be written as follows.

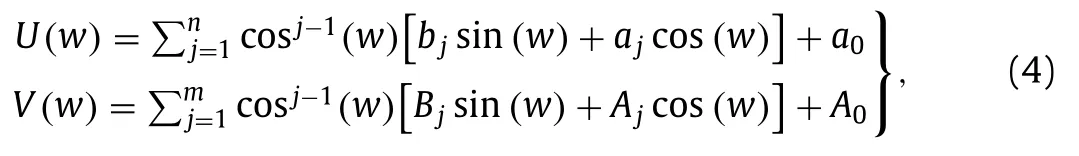
where w = w (η) satisfies a simplified form of the sine-Gordon equation, written as [27] :

Equation (5) admits the following solutions [46] :

and

The derivation procedure is included in Appendix-1 .

With the help of Eqs.( 5-7 ), the solutions of U(η) and V (η)specified by Eq.(4) can be presented as follows:

and

Step 3: By using the homogeneous balance principle between linear and nonlinear terms of the Eq.(3) , one can yield the value of n and m .Plugging the values of n and m into Eq.(4) along with Eq.(5) , we collect a nonlinear system of equations in terms of si nj(w ) and co sj(w ) .Setting the coefficients of si nj(w ) , co sj(w ) ,and its product to zero, we have systems of equations.Solving these systems of equations, the values of aj, bj, Aj, Bj, k and ω are obtained.By inserting the values of aj, bj, Aj, Bj, k and ωin Eq.(8) and Eq.(9) , one can determine the solitary, and singular wave solutions of Eq.(3) .Finally, by putting back the complex transform E( x, t ) = eiθU(η) , N( x, t ) = V (η) , where θ= kx + ωt, and η= px + rtto the obtained solutions, then we have found the solitary and singular wave solutions of Eq.(1) .

By setting the complex travelling wave transformation as:

where the arbitrary constant k, ωand care to be determined.

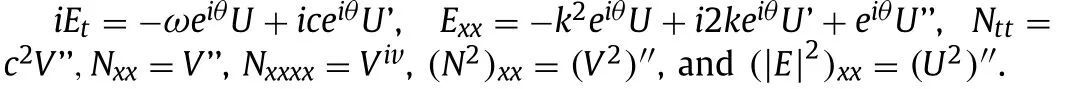
By plugging the above transformation into Eq.(1) , one can obtain the following system:

Integrating two times with respect to ηin Eq.(13) and the integration constants are taken zero, we have

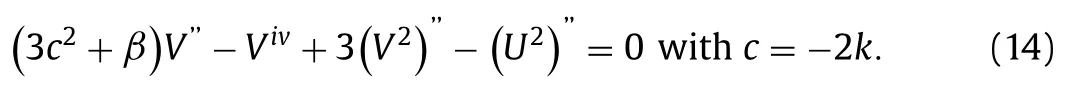
Therefore, Eq.(12) and Eq.(14) can be rearranged after putting c = -2 k as follows:

where the prime stands for the derivative with respect to η.

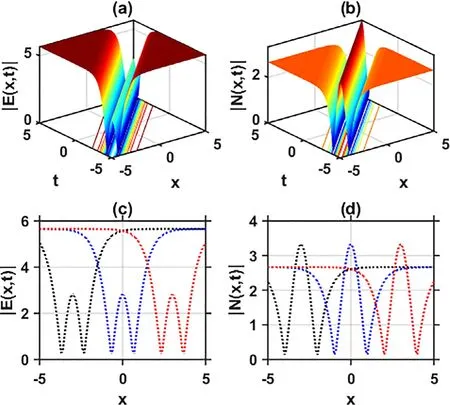
Fig.2.(a)-(b) 3D plots of the solutions | E( x, t )| and | N( x, t )| specified by Eq.(21) , and (c)-(d) 2D plots of (a)-(b), respectively.The dotted black, blue, and red lines indicate the variations of the mentioned solutions along t = -3 , t = 0 , t = 3 , respectively.

In order to determine the soliton and other solutions, the sGEM is applied to the gSBq equations.In this regard, the homogeneous balance principle is applied between the highest order derivative terms and nonlinear terms in Eq.(15) , yields m = 2 and n = 2 .It is supposed that the formal series solution of Eq.(15) with the help of Eq.(4) , Eq.(8) , and Eq.(9) , we have:

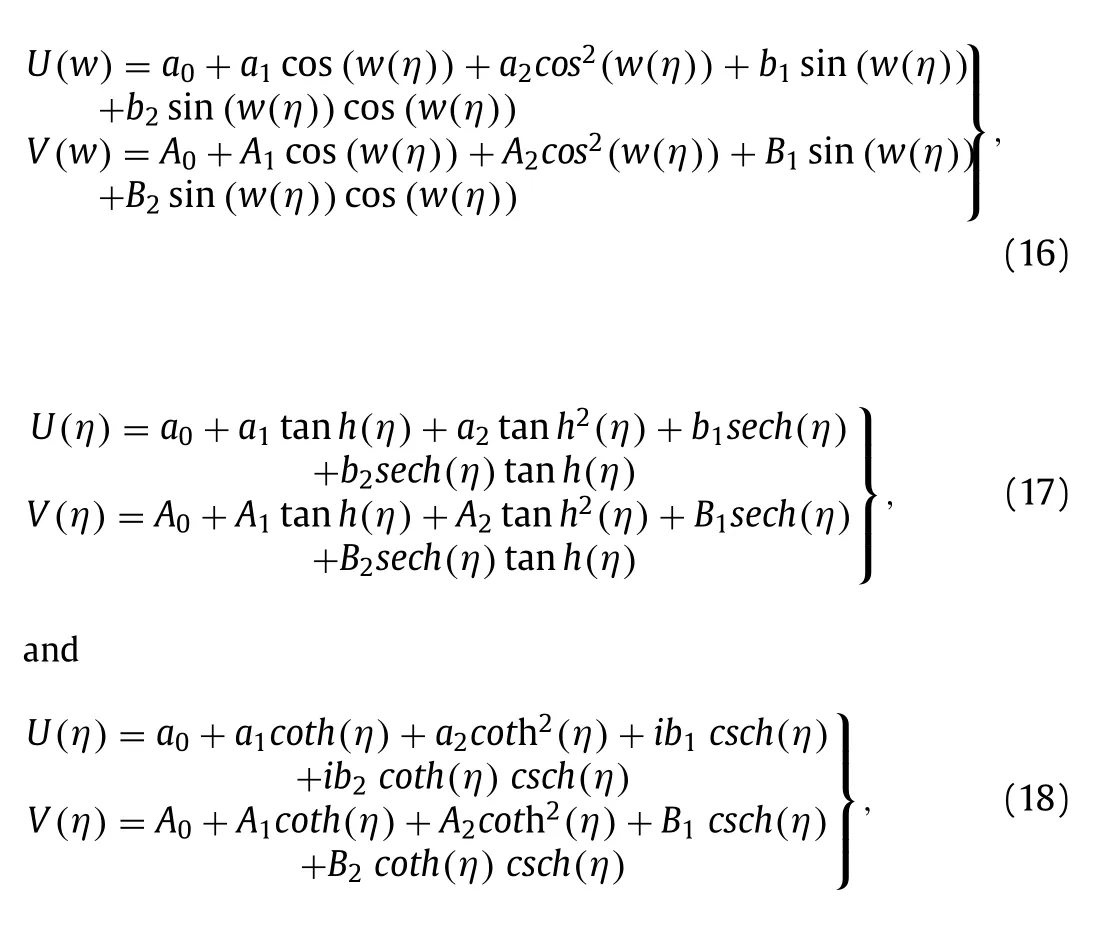
where either a2or b2or A2or B2or a1or b1or A1or B1may be zero, but not all of them become zero simultaneously.

By plugging Eq.(16) and its derivatives along with Eq.(5) into Eq.(15) , we obtain a nonlinear algebraic system of equations.Then,to solve the system of equations with the aid of symbolic computation Maple, the following sets of solutions are attained:

Fig.3.(a)-(b) 3D plots of the solutions | E( x, t )| and | N( x, t )| specified by Eq.(25) , and (c)-(d) 2D plots of (a)-(b), respectively.The dotted black, blue, and red lines indicate the variations of the mentioned solutions along t = -3 , t = 0 , t = 3 , respectively.

One can explore the following solutions of Eq.(1) via Eqs.(17) and (18) along with Eq.(10) :

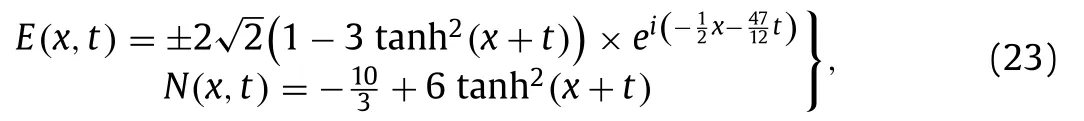
and

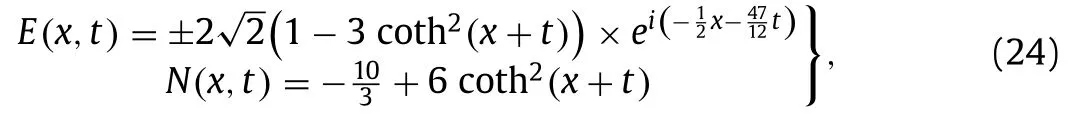
Set 4

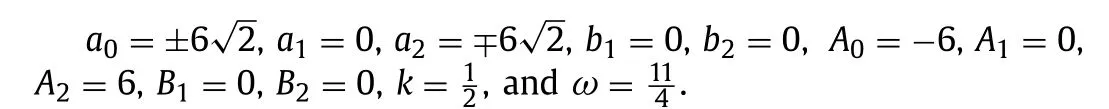
One can determine the following solutions of Eq.(1) via Eqs.(17) and (18) along with Eq.(10) :

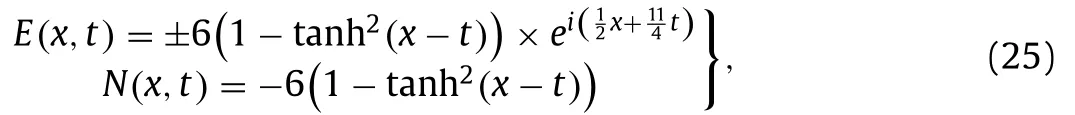
and

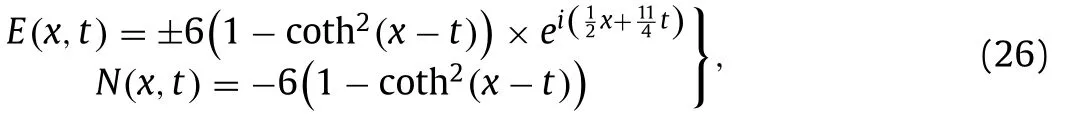
Set 5

One can generate the following solutions of Eq.(1) via Eqs.(17) and (18) along with Eq.(10) :

and

Set 6

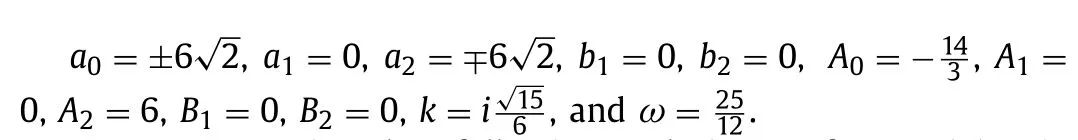
One can attain the following solutions of Eq.(1) via Eqs.(17) and (18) along with Eq.(10) :

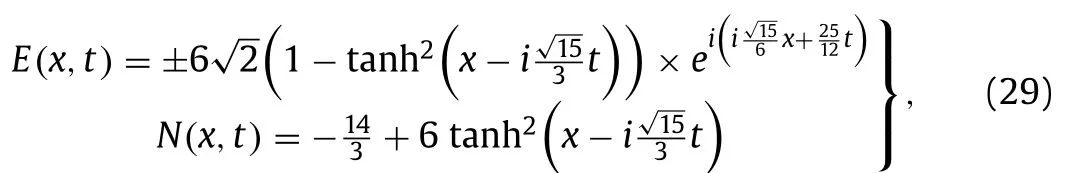
and

Set 7

One can find the following solutions via Eqs.(17) and (18) along with Eq.(10) :

and

Fig.4.(a)-(b) 3D plots of the solutions | E( x, t )| and | N( x, t )| specified by Eq.(29) , and (c)-(d) 2D plots of (a)-(b), respectively.The dotted black, blue, and red lines indicate the variations of the mentioned solutions along t = 0 , t = 1 , t = 2 , respectively.

Set 8

Set 10

Fig.5.(a)-(b) 3D plots of the solutions | E( x, t )| and | N( x, t )| specified by Eq.(31) , and (c)-(d) 2D plots of (a)-(b), respectively.The dotted black, blue, and red lines indicate the variations of the mentioned solutions along t = -2 .5 , t = 0 , t = 3 , respectively.

Fig.6.(a)-(b) 3D plots of the solutions | E( x, t )| and | N( x, t )| specified by Eq.(33) , and (c)-(d) 2D plots of (a)-(b), respectively.The dotted black, blue, and red lines indicate the variations of the mentioned solutions along x = -3 , x = 0 , x = 3 , respectively.

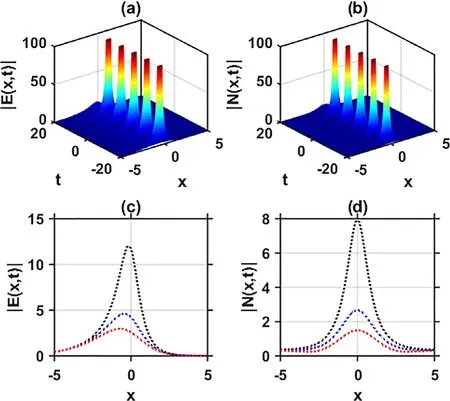
Fig.7.(a)-(b) 3D plots of the solutions | E( x, t )| and | N( x, t )| specified by Eq.(35) , and (c)-(d) 2D plots of (a)-(b), respectively.The dotted black, blue, and red lines indicate the variations of the mentioned solutions along t = -3 , t = 0 , t = 3 , respectively.

For our convenience, to solve the system of equations, we have considered α= -1 and β= 1 .

In order to understand the proper significance of the gSBq equations via some attained soliton solutions, three-dimensional(3D) and two-dimensional (2D) graphs are presented.The sGEM is fruitfully executed by constructing various types of solitary wave solutions to the gSBq equations.It is mentioned earlier that for the specified governing gSBq equation given by Eq.(1) has been investigated previously by a variety of analytic methods [15-31] .According to their study, they have not reported the combo brightdark, W -shaped, M-shaped, and periodic waves solutions.However, in this research study, bright, dark, combined dark-bright,W -shaped, M-shaped, singular, combined singular, periodic, singular periodic wave solutions, and other soliton solutions are constructed to the gSBq equations via the sGEM.According to our knowledge, it can be assured that all the combined dark-bright, W -shaped, M-shaped, combined-singular, and periodic wave solutions have been discussed and investigated in this paper for the first time.It also should be mentioned that the validity of the extracted solutions is examined by substituting each exact solution back into the original equation.The dark solitons, bright solitons, combined dark-bright solitons, W -shaped solitons, M-shaped solitons, singular solitons, combined singular solitons, and periodic wave solutions of Eq.(1) are represented in Eqs.( 19-40 ).It is noteworthy to mention here that all of these generated solutions are specified by Eqs.( 19-40 ) have unique physical significance.In order to have a good understanding of the hidden properties of the gSBq equations, the 3D and 2D line graphs can be presented among the explored soliton solutions specified by Eqs.( 19-40 ).The outlook of the explored soliton solutions prescribed by Eqs.(19) , (21) , (25) ,(29) , (31) , (33) , and (35) can be perceived in the 3D and 2D graphs at different values of t, as seen in Figs.1-7 , respectively.Fig.1 ,Fig.4 , Fig.5 , and Fig.7 represent the t-periodic wave solutions.On the other hand, Fig.2 , Fig.3 , and Fig.6 display the W -shaped,bright, and M-shaped soliton solutions, respectively.The propagation behavior of the solitons is displayed under the 2D graphs.It is clear from the graphical outputs that the procedure of the sGEM will contribute to other related equations for obtaining some novel soliton solutions.Therefore, it is quite evident that the derived results in this work provide new knowledge to the existing literature because of its importance in many fields of optics and physics.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix-1.Appendix-1

Consider the following sine-Gordon equation [46] :

where u = u ( x, t ) and τis a constant.Introducing the transformation u ( x, t ) = U(ξ) where ξ= μ( x -ct ) , reduces Eq.(41) to the following nonlinear ordinary differential equation

Multiplying U ’ by both sides of Eq.(42) and integrating it, once gives

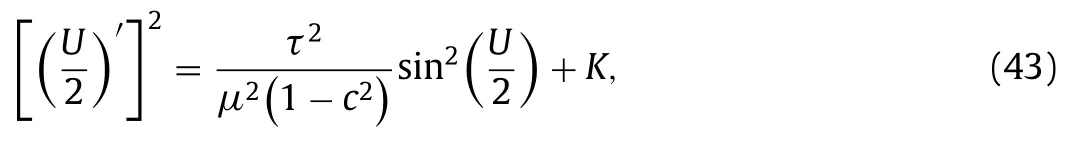
where Kis an integration constant.

If we take ϑ = 1 in Eq.(44) , we find:

This is a simplified form of the sine-Gordon equation.Therefore,Eq.(45) has the following solutions:

and

The detailed transformation procedure of the sGEM can be found in ref.[46] .Eqs.46 ) ( (47)